Learning to play Coup with DQN

I've recently been having a lot of fun playing the board game Coup. Since being introduced to it, I've put a lot of thought towards potential strategies and methods to optimize my chances of winning. Having just taken a machine learning class, and taking an artificial intelligence class this Summer, I wondered if I could solve this problem with computers.

Before this, I have had no experience with any reinforcement learning techniques, but they always seemed interesting to me. While supervised learning learns the connections between data and their labels, reinforcement learning has to learn connections between states, actions, and rewards, a seemingly more complex (at least to me) problem. And so, I set out to model the game of Coup and train an agent to play it.

What exactly is Coup?

Coup is a strategic board game that immerses players in a dystopian universe, where they engage in political intrigue, deception, and manipulation. The game is designed for 2 to 6 players and typically lasts around 15 minutes.

In Coup, players assume the roles of powerful figures, such as Dukes, Assassins, Captains, Ambassadors, and Contessas, each with unique abilities. The objective of the game is to eliminate opponents' characters and be the last player standing.

The game revolves around a set of character cards, which players possess and keep hidden from others. These character cards grant special actions or abilities that players can use strategically to deceive opponents or protect themselves. However, there is an element of bluffing involved, as players can always claim to have a certain character card even if they don't.

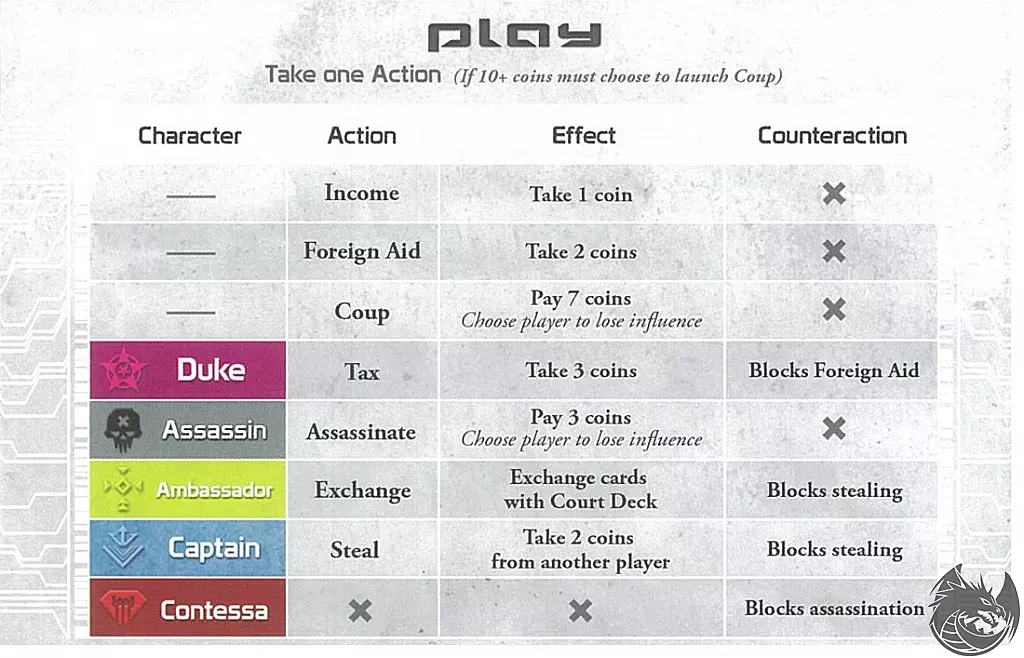
On their turn, players can take one of several actions as described in the chart above. Other players can choose to take a counteraction to block an action, or can call a bluff if they do not believe the original action was taken by a player who has the corresponding role. The game unfolds with players making tactical decisions, attempting to deduce opponents' identities, and using their abilities to gain advantages while avoiding exposure.

Coup's gameplay is fast-paced and filled with uncertainty, as players must navigate a web of deceit, determine who to trust, and make strategic moves to outwit opponents. With its blend of strategy, deduction, and bluffing, Coup offers an exciting and challenging experience for both casual and experienced gamers. But how about a reinforcement learning agent? Will I be able to train my agent to become an excellent Coup player?

A Brief Introduction to Reinforcement Learning

In my initial research on reinforcement learning, I learned about two approaches: model-based and model-free reinforcement learning. Model-based and model-free reinforcement learning are two different approaches used in the field of machine learning for solving sequential decision-making problems. The main distinction between them lies in how they handle the underlying environment dynamics.

Model-based v.s. Model-free

Model-based reinforcement learning involves building an explicit model of the environment, which captures the transition probabilities and rewards associated with different states and actions. This model is used to simulate and plan ahead, allowing the agent to make informed decisions. The agent uses the model to predict the consequences of its actions and learns from those predictions. Model-based methods often involve techniques such as dynamic programming or Monte Carlo tree search to compute optimal policies.

On the other hand, model-free reinforcement learning does not require an explicit model of the environment. Instead, the agent learns directly from interaction with the environment, without explicitly estimating transition probabilities or rewards. It focuses on estimating the value or action-value functions, which represent the expected future rewards for different states or state-action pairs. Model-free methods typically rely on trial-and-error learning and exploration strategies to improve their policies over time. Popular model-free algorithms include Q-learning, SARSA, and deep reinforcement learning methods like DQN or DDPG.

Consider a model-based and a model-free approach to learning Coup. In model-based learning, the agent would start by observing the rules of the game, the actions available, and the outcomes associated with those actions. It would then build a model of the game, including the probabilities of different actions succeeding or failing and the resulting game state changes. The agent could use this model to plan its moves, considering the potential consequences of each action and selecting the optimal strategy based on its predictions.

In contrast, a model-free learning agent would start with no prior knowledge of the game's rules or dynamics. It would interact with the game environment, making random or exploratory moves and observing the outcomes. By using a trial-and-error approach and updating its value or action-value function based on the observed rewards, the agent would gradually learn which actions lead to favorable outcomes and adjust its policy accordingly. Over time, the model-free agent would refine its strategy through repeated gameplay.

Q-Learning

For this project, I decided to use a model-free approach; specifically I used Q-learning. Q-learning learns an optimal policy by estimating the action-value function, \(Q(s, a)\), which represents the expected cumulative reward for taking action \(a\) in state \(s\).

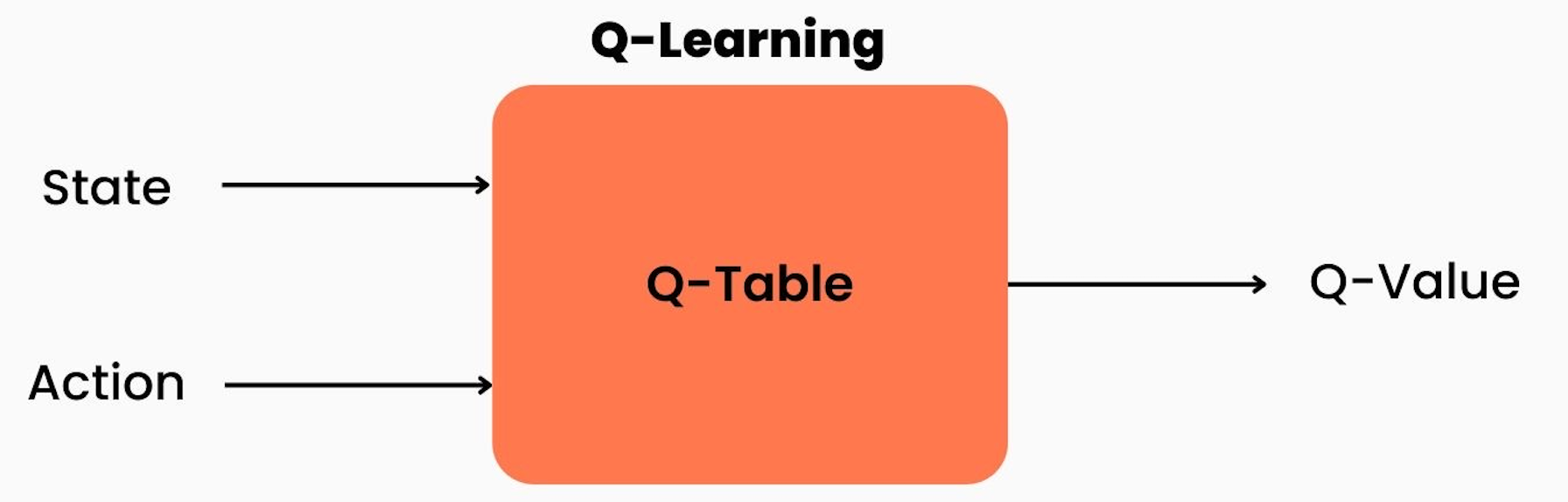
The algorithm iteratively updates the Q-values based on the observed rewards and uses an exploration-exploitation strategy to balance exploration of new actions and exploitation of learned knowledge. The key update rule in Q-learning is the Bellman equation, which states that the Q-value of a state-action pair should be updated based on the maximum expected future reward achievable from the next state. The Bellman equation is the following:

\(Q(s_t,a_t)=\mathbb{E}\left[r_{t+1}+\gamma r_{t+2}+\gamma^2r_{t+3}+\ldots\middle|s_t, a_t\right]\),

where \(s_t\) is the state at time \(t\), \(a_t\) is the action at time \(t\), \(r_t\) is the reward at time \(t\), and \(\gamma\) is the discount factor.

One clear issue with this approach to Q-learning is that it requires a table of Q-values corresponding to all state-action pairs. However, in a game like Coup, there are too many states for this to be feasible. Thus, I utilized a different type of Q-learning: deep Q-learning.

Deep Q-learning combines traditional Q-learning with deep neural networks. Instead of explicitly storing and updating Q-values in a tabular form, deep Q-learning approximates the Q-values using a deep neural network, referred to as a Q-network. The Q-network takes the state as input and outputs Q-values for all possible actions.

The training process involves feeding the current state to the Q-network, selecting the action with the maximum Q-value (or using an exploration strategy, more on that later), and receiving the corresponding reward and next state. The loss is computed as the mean squared error between the predicted Q-value and the target Q-value, which is obtained by applying the Bellman equation.

Deep Q-learning offers several advantages over traditional Q-learning:

• It can handle high-dimensional state spaces by leveraging the powerful representation learning capabilities of deep neural networks.
• The Q-network generalizes across similar states, allowing the agent to make informed decisions in unseen states.
• Deep Q-learning enables end-to-end learning, where the agent learns both the optimal policy and the feature representations simultaneously, eliminating the need for manual feature engineering.
• Deep Q-learning can handle continuous action spaces by employing function approximators, such as DDPG (this won't be relevant to Coup, but I found it interesting).

Exploitation and Exploration

Consider the case where an agent learns that taking the action income in Coup always yields a reward of one coin. If an agent were to only exploit its current knowledge base, it may never do any other action, but if it has to explore other options it might discover the usefulness of trying other actions. This dilemma is often called exploration vs exploitation. Exploitation and exploration are two crucial aspects of reinforcement learning that help strike a balance between utilizing the learned knowledge and discovering new information.

Exploitation refers to the strategy of leveraging the current knowledge to exploit actions that are known to yield high rewards. It involves selecting the actions that have the highest estimated Q-values based on the learned policy. Exploitation is essential to maximize the agent's performance in known situations and exploit the best actions based on its current knowledge.

Exploration, on the other hand, involves taking actions that deviate from the known optimal policy to gather new information about the environment. It aims to explore uncharted regions of the state-action space to discover potentially better actions that may lead to higher rewards. Exploration is crucial in the early stages of learning or when facing uncertain or changing environments.

Deep Q-learning addresses the exploration-exploitation dilemma by employing an \(\epsilon\)-greedy strategy. During training, the agent chooses actions based on a balance between exploration and exploitation. With a probability of \(\epsilon\), the agent selects a random action, allowing for exploration and the discovery of new states and actions. This random action selection helps to explore the state-action space more thoroughly and gather valuable experience. However, with a probability of \(1-\epsilon\), the agent selects the action with the highest Q-value, exploiting the current knowledge and maximizing the expected rewards.

As training progresses and the agent's knowledge improves, \(\epsilon\) can be gradually decreased to shift the focus towards exploitation. This strategy ensures that the agent initially explores extensively to learn about the environment but gradually exploits the learned knowledge to make optimal decisions. It strikes a balance between exploring new possibilities and exploiting the most promising actions based on the current knowledge.

In this way, deep Q-learning combines the power of deep neural networks to approximate Q-values and the epsilon-greedy strategy to handle the exploration-exploitation trade-off. By adjusting the exploration rate during training, the agent can effectively navigate the reinforcement learning problem, gradually shifting from exploration to exploitation as it gains more knowledge and improves its performance.

Results of my Q-Learning Agent

After recreating Coup in Python, I created four simple player archetypes for my Q-Learning Agent to play against and learn from. They are the following:

• Random: plays completely randomly
• Truth: plays completely randomly within the confines of truth
• Greedy: plays greedily, trying to maximize its own coins and minimizes its opponents' cards
• Income: only takes income or assassinates

The results of my agents varied depending on which archetypes they were trained against, so I tried many different variations.

Training Graphs

The following are some training graphs for various models I trained. Not all models were included in this section, although they can be found in the Github repository here.

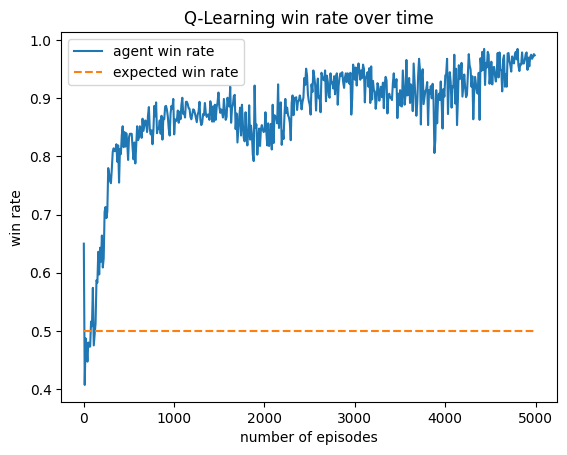
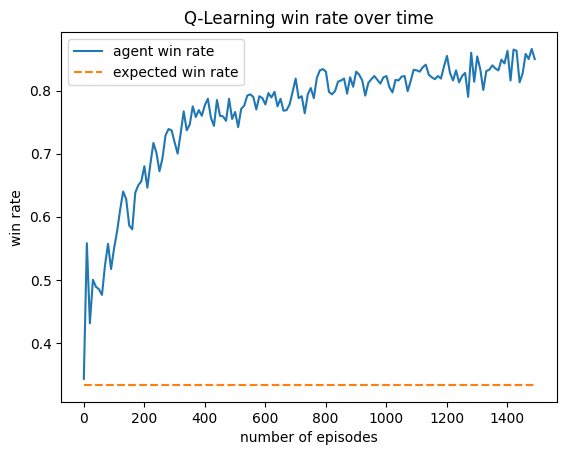
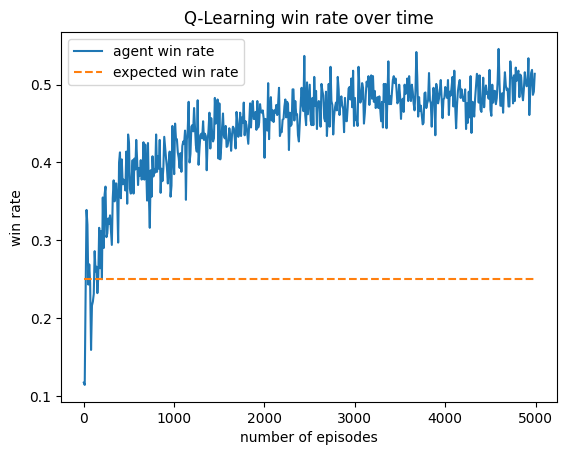
Results Charts

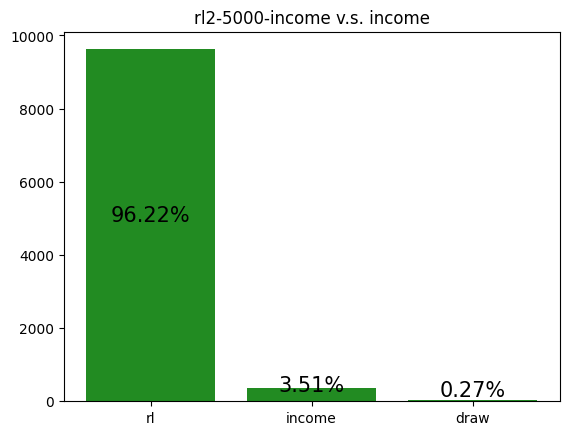
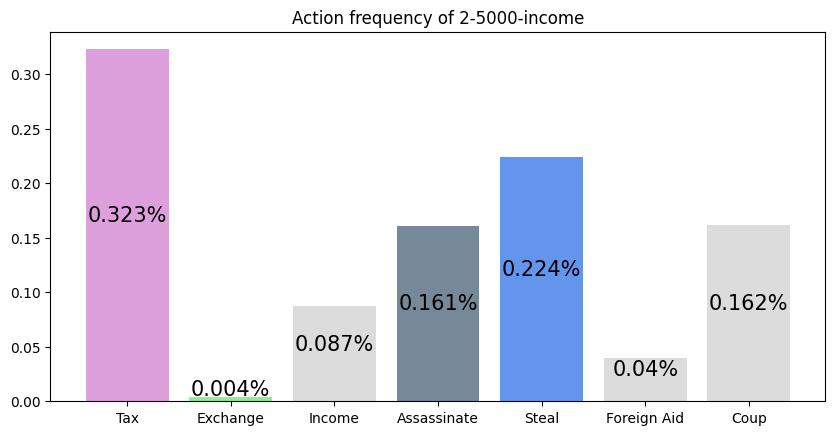
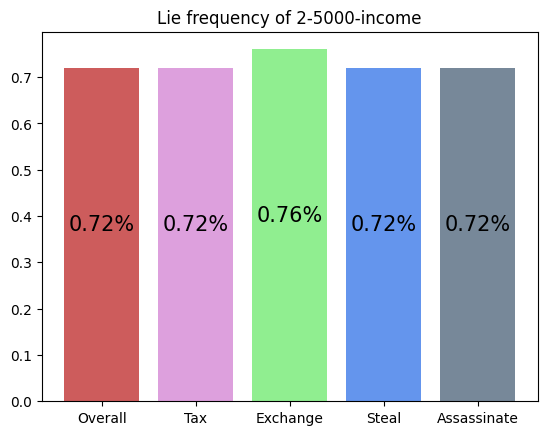
This agent was trained against an income player. It seems to have realized it could outpace the income player by performing Tax and Steal, thus achieving a very high win rate.

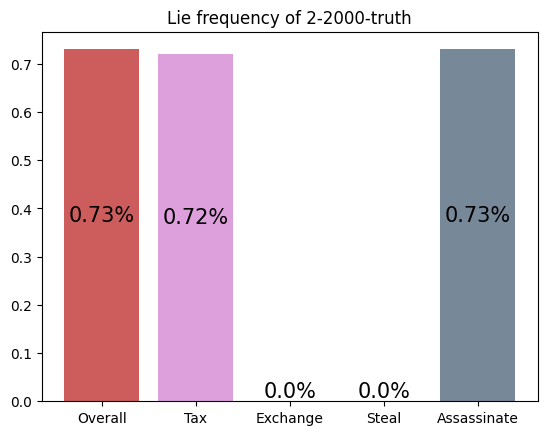
This agent was trained against a truth player, but the simulation was against a greedy player. Here, the agent loses by a wide margin, performing worse than a random player (see the Appendix for archetype v.s. archetype simulations). It appears to assassinate much more than it should, a strategy good against a truth player, but not a greedy one.

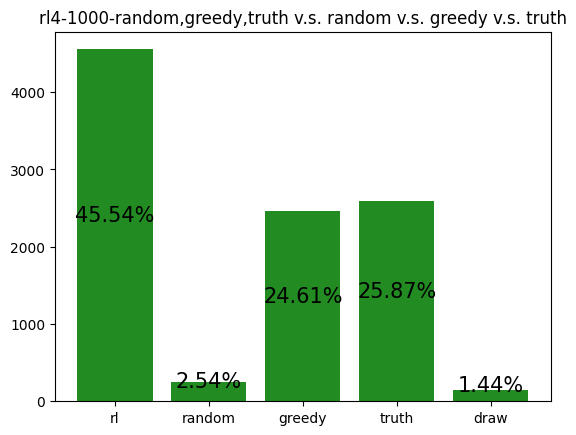
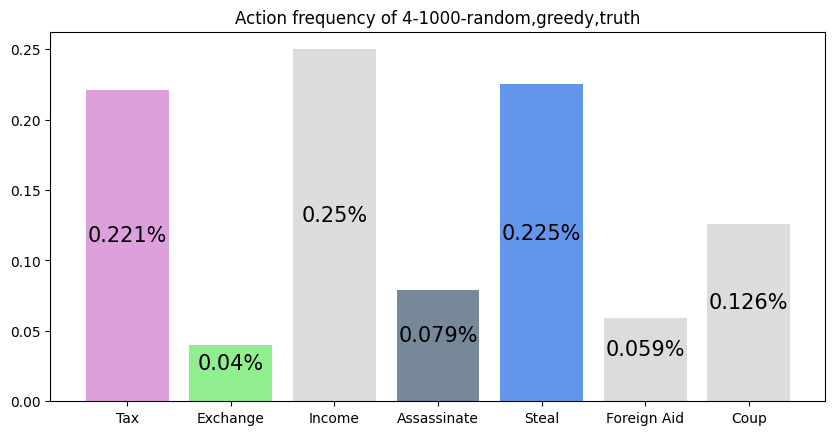
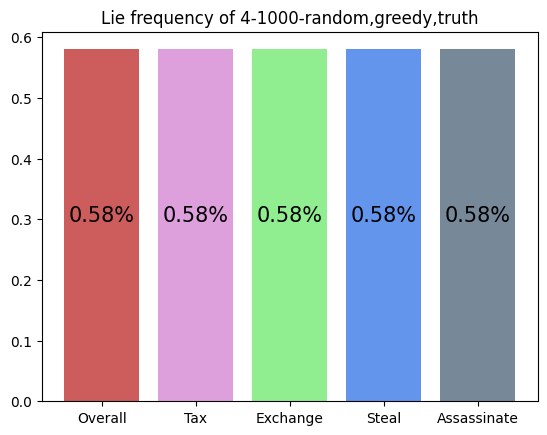
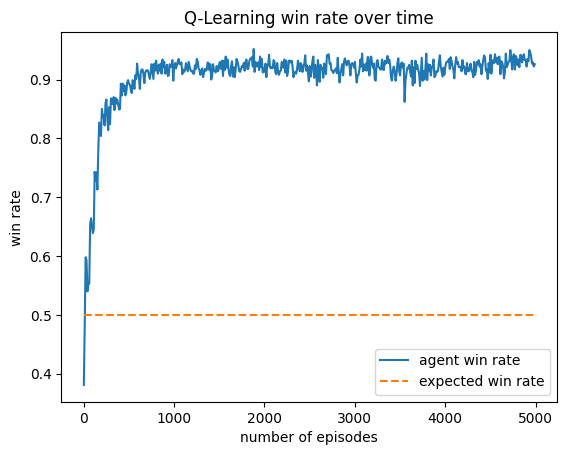
This agent was trained against a random, greedy, and truth player. It wins much more than expected (25%). It favors choosing Tax, Income, and Steal, and uniformly lies about all of its actions. This makes it difficult to block the agent, as its actions seem to not depend on its cards.

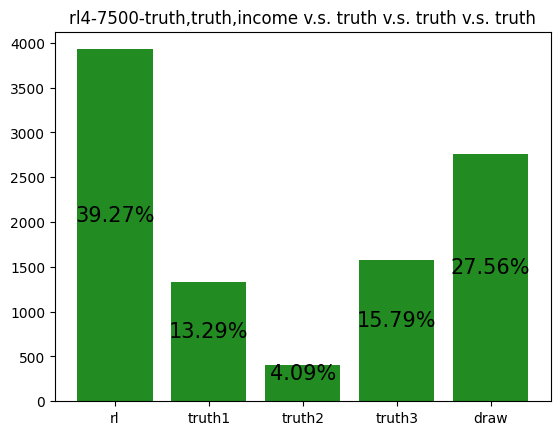
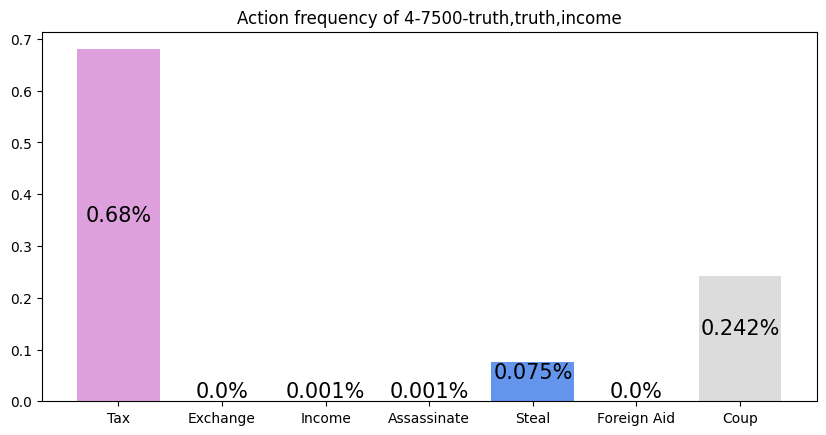
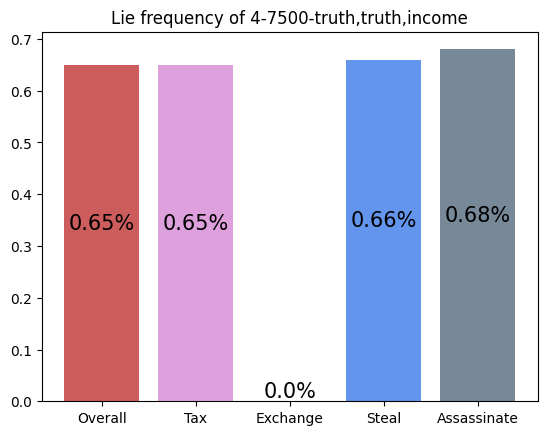
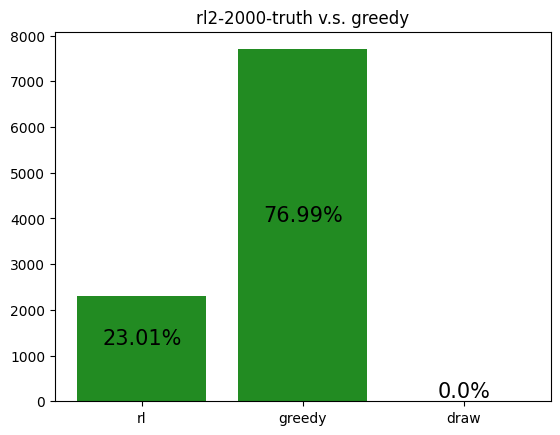
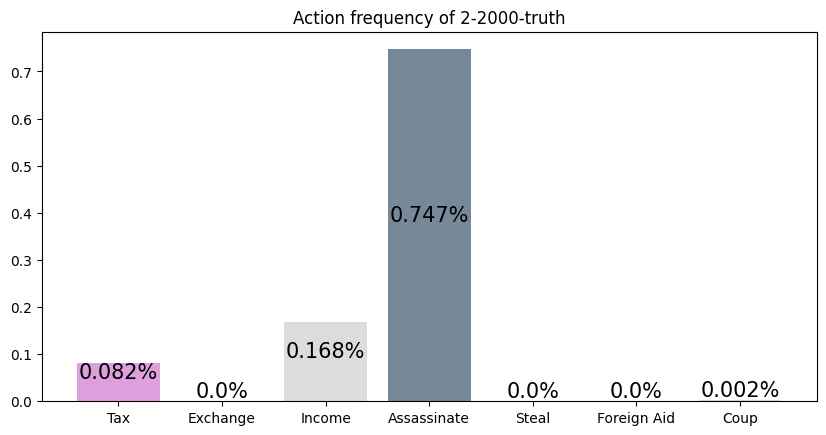
This agent was trained against three truth players. It performs exceptionally well, winning over half of all games that don't end in a draw. It appears to have learned to repeatedly take Tax regardless of its cards, and then Coup its opponents. This makes sense against Truth players, as they never block Tax. I find it interesting that so many games end in a draw. For my simulations, I defined a draw as a game that was not resolved in 50 turns. I noticed that increasing my turn limit had little effect on the draw rate, so it appears that this matchup is prone to infinite loops.

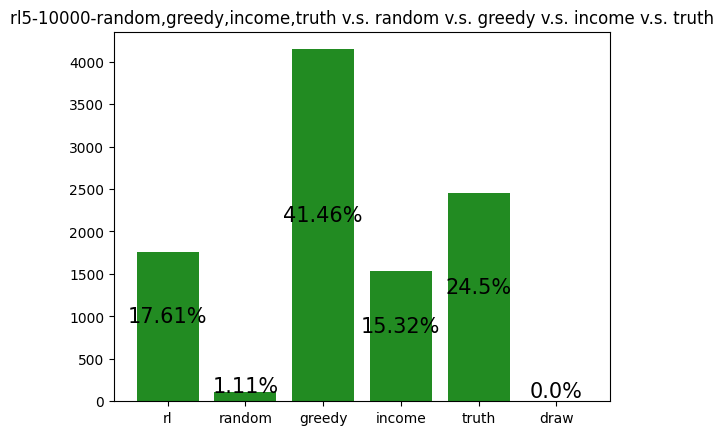
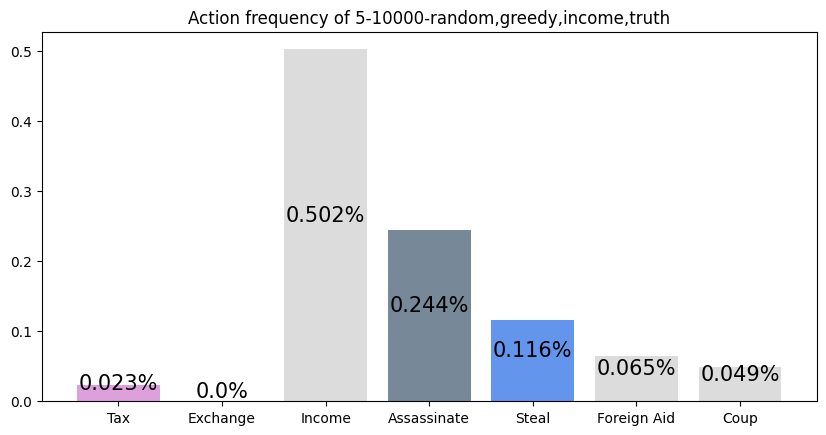
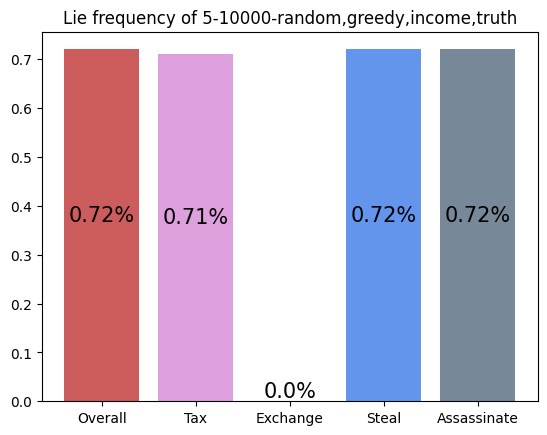
This agent was trained against a random, greedy, income, and truth player. It performs slightly worse than expected (20%), but this makes sense with the context that the greedy player dominates. It appears as if this player learned to play like a slightly more optimal income player, as its most two common actions are Income and Assassinate.

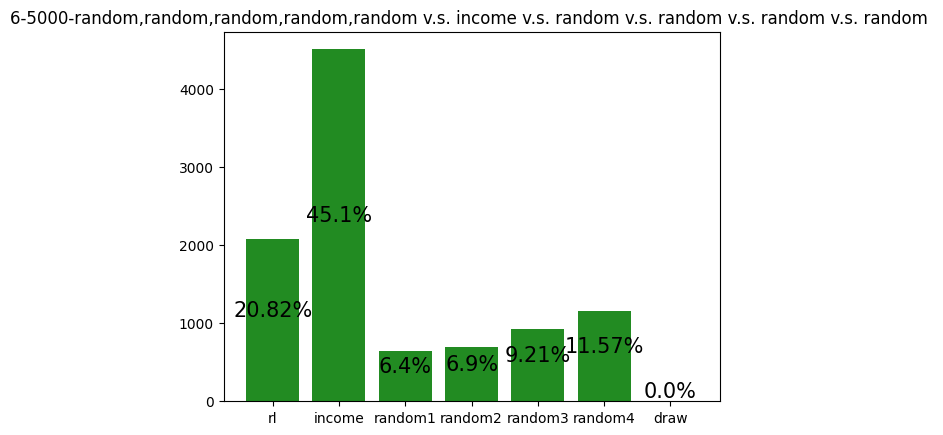
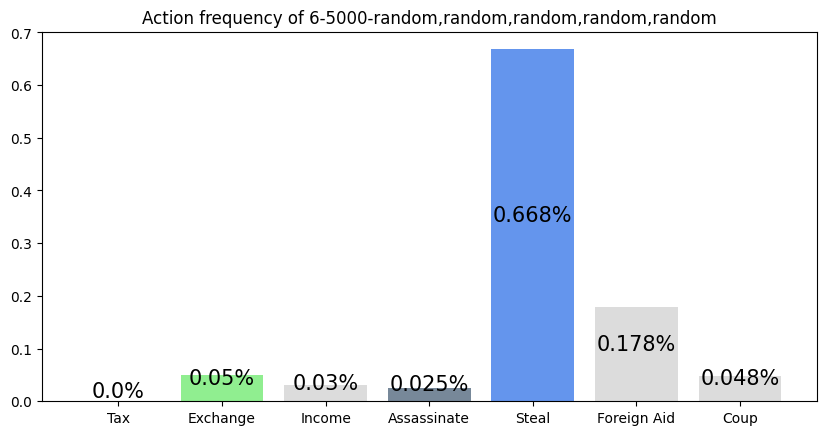
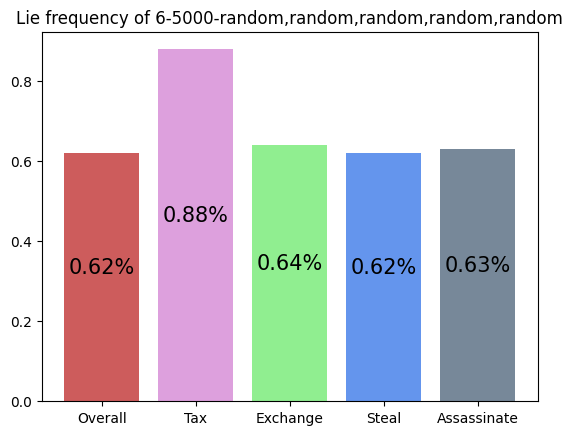
This agent was trained against five random players, but the simulation was against an income player and four random players. Although it still performs slightly above expected (16.7%), compared to its training graph (not shown in this article), its performance is lower. The inclusion of a 'more advanced' archetype seems to have hurt the feasibility of this agent's strategy of performing Steal, Foreign Aid, and Coup. Since income players block Steal against themselves when they can, it is more difficult for the agent to win.

Conclusion

This has been an incredibly fun project where I've learned a lot. Not only have I learned a lot about how to play Coup and the different strategies that one may take, I have also learned a lot about reinforcement learning, specifically Q-Learning. This project has made me excited to look into other areas where similar techniques may prove useful.

Additionally, there are so many more things for me to continue looking into in this project. For example, here are some of the ideas I've thought of already:

• Experiment with different Neural Network architectures for the Q-Network
• Deploy different reward functions
• Utilize the game history as an input to the RL agent's Q-Network
• Learn the block, dispose, and keep functions (see the Appendix)
• Train the RL agents against each other
• Build a website / UI to play against the different agents or watch them play
• Explore the differing win rates depending on start position

But for now, I think I'm going to take a break from this project. Thanks for reading, and take a look at the repository here if you want to learn more about the code and how I programmed everything. Additionally you can also read the appendix below for a quick summary.

Appendix: Modeling Coup in Python

In order for an agent to learn, it must exist in an environment where it can play the game. Thus, I needed to create my own version of Coup. I chose to do this in Python, as I would later use the PyTorch module to train the Q-Learning agent.

There are two main classes needed to simulate a game of Coup: the Game class and the Player class. These classes communicate to each other at various points in a game loop in order to simulate a full game.

The Game Class

A Game instance is created by passing in a list of players. Each instance has a game_state and history variable. The following is the init method of the Game class:

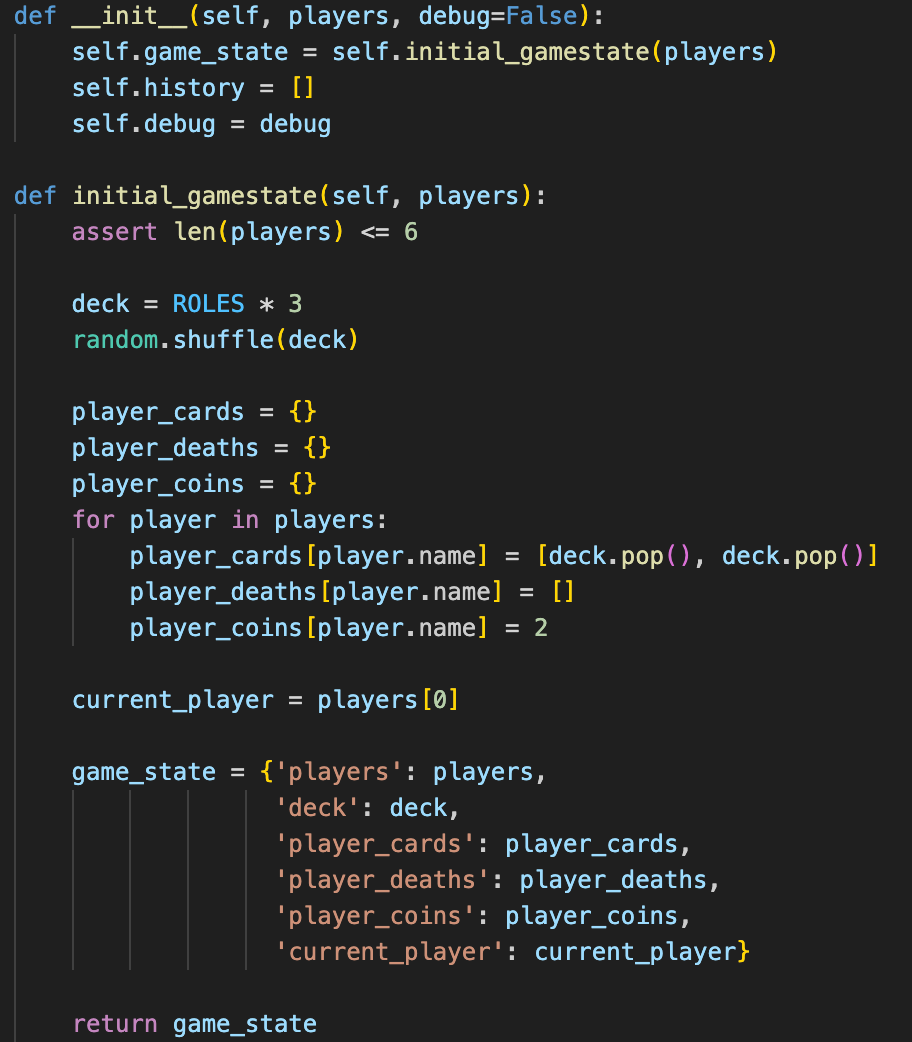
The game_state variable is a dictionary containing the relevant information of the current state of the game, as seen above. It is updated after each turn, after actions have been made. The history variable is a list containing tuples of previous game_states and turns.

Turns, actions, and blocks are both represented under the hood by triples.

• turn: \((action, block\_1, block\_2)\)
• action: \((sender, reciever, type)\)
• block: \((blocker, attempt\_block?, lie\_or\_counteraction?)\)

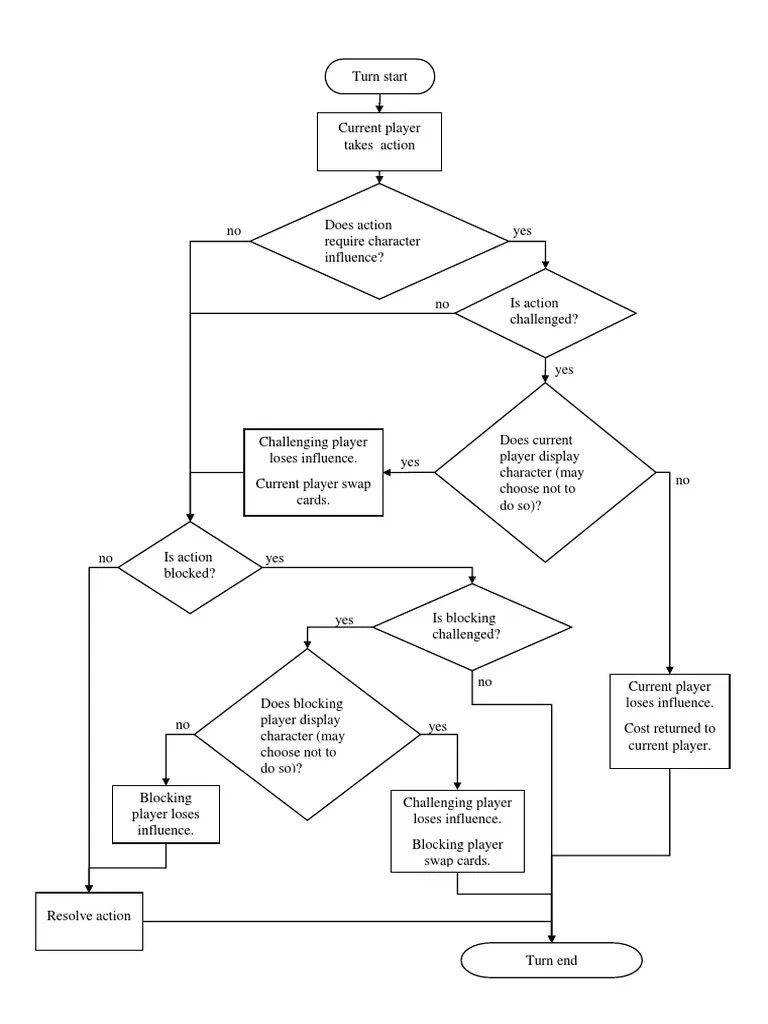
The most important method in the Game class is simulate_turn. By calling game.simulate_turn(), the turn of the current player's turn is played, querying the current player for an action, along with the other players blocks. Then, it applies the logic of the game in order to update the state. The following is the simulate_turn method:

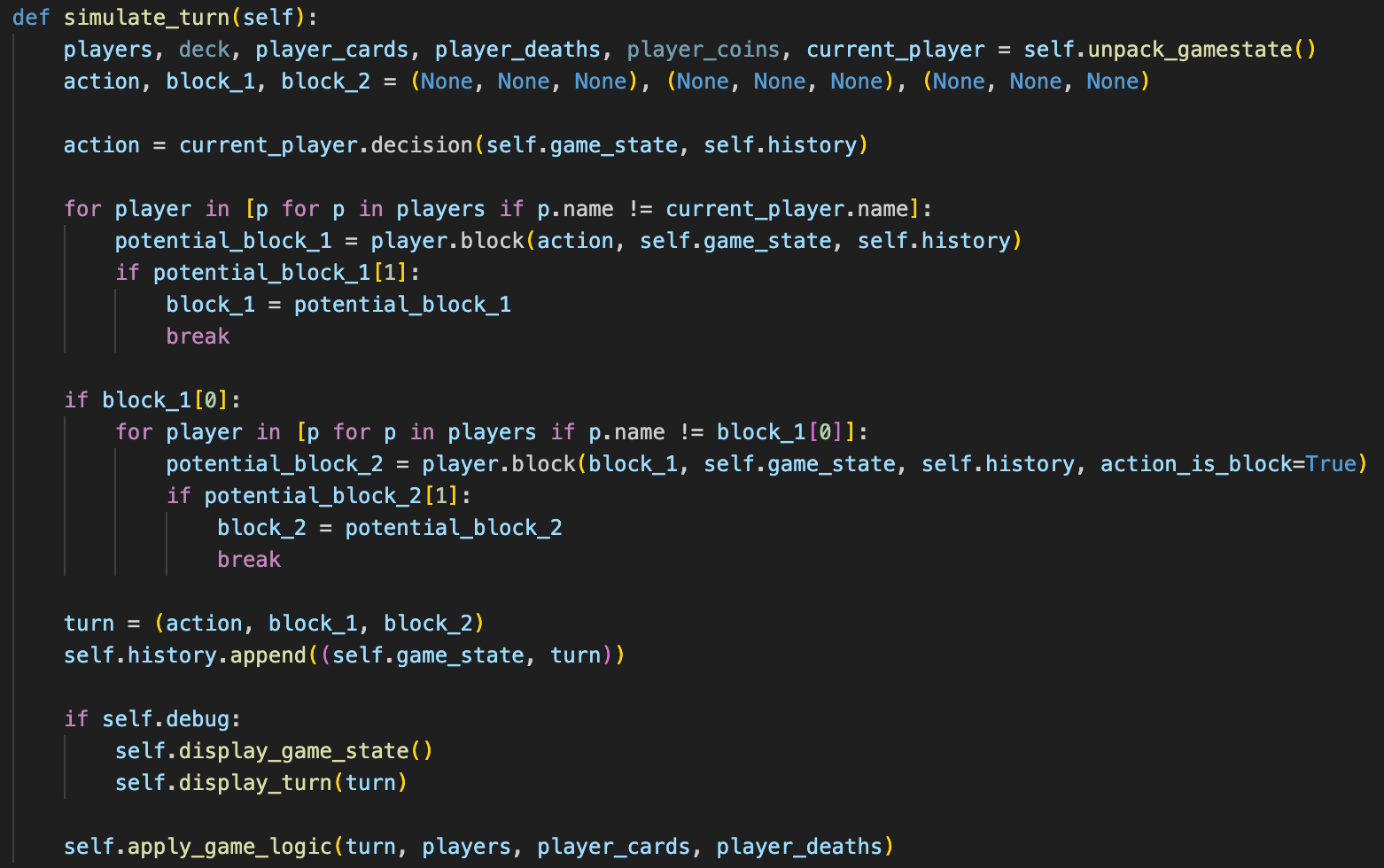
The Player Class and Player Archetypes

A Player instance is defined using four functions as inputs: a decision function, block function, dispose function, and keep function. The following is the purpose of each function.

• \(decision\_fn\): returns actions based on the game_state and history
• \(block\_fn\): returns blocks based on the action, game_state, and history
• \(dispose\_fn\): returns the index of the cards to lose when necessary
• \(keep\_fn\): returns the indicies of the cards to keep after exchanging

I designed four main types of players, called archetypes. They are the following:

• Random: every function is completely random
• Truth: decision and block take random actions that tell the truth; dispose and keep are completely random
• Greedy: decision and block take 'greedy' actions that maximize their own coins and minimize other players' cards; dispose and keep are completely random
• Income: decision only takes either income or assassinate regardless of lies, blocks only when telling the truth and when action is directed at self; dispose and keep are completely random

The following are simulations of archetypes against each other:

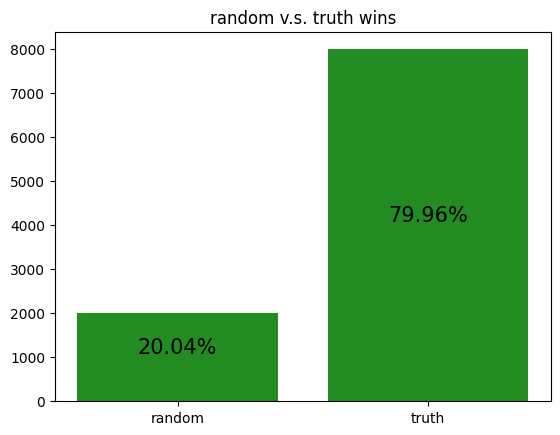
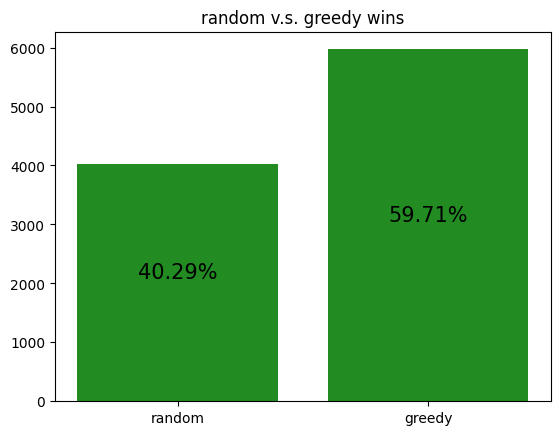
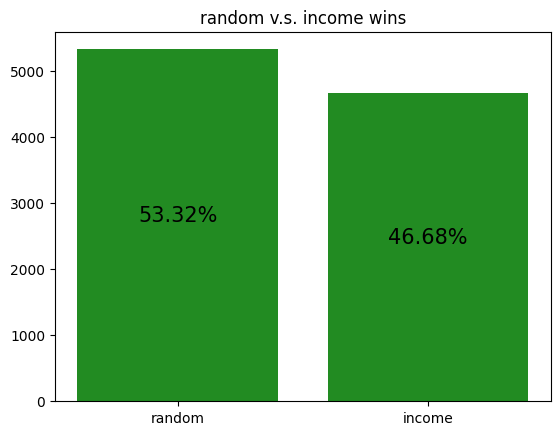
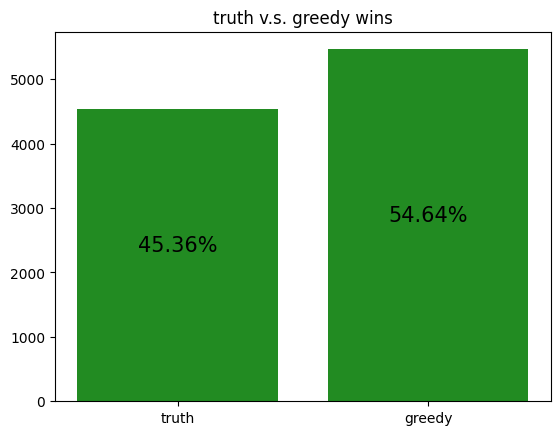
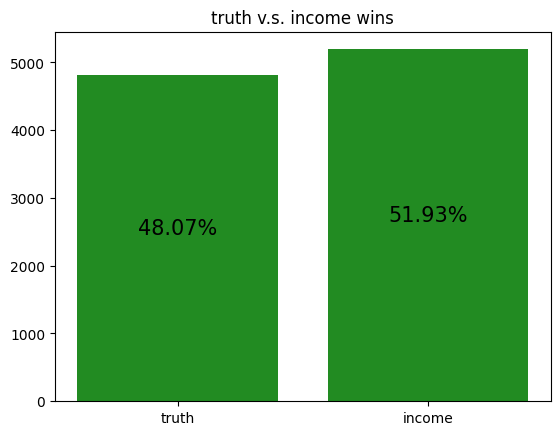
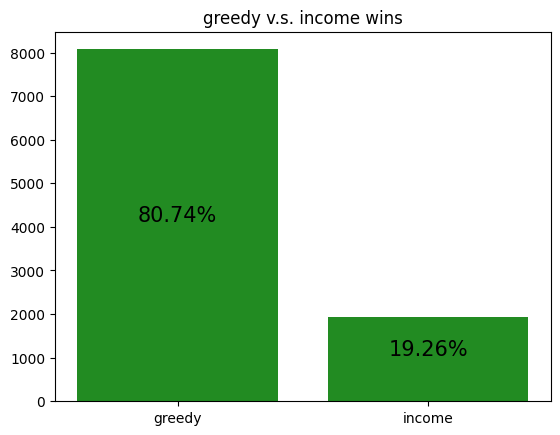
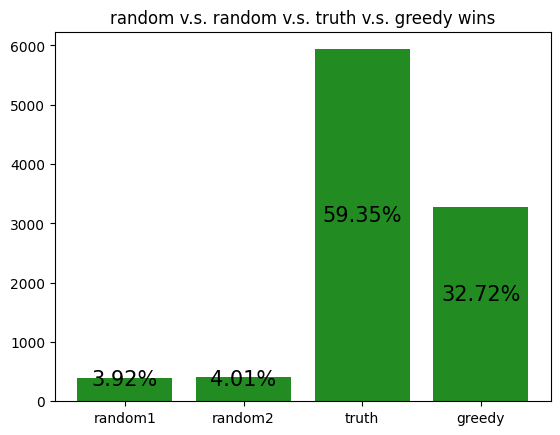
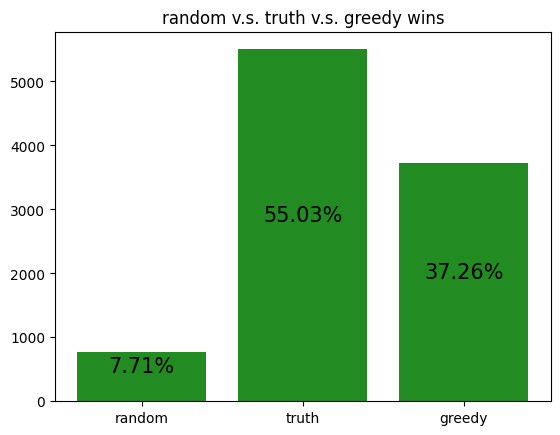
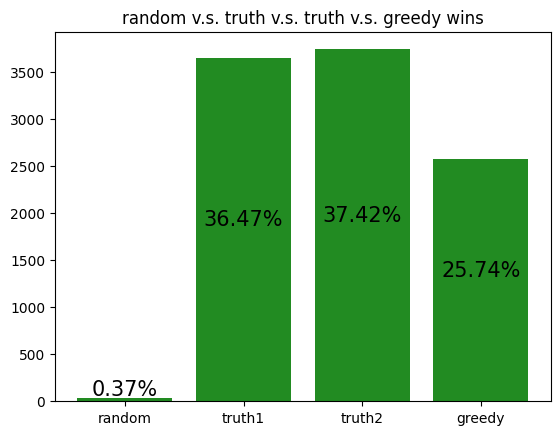
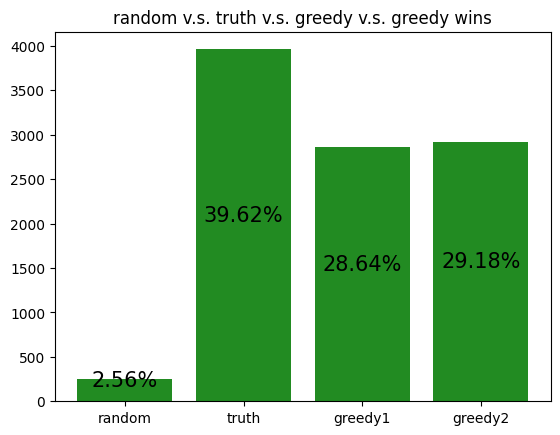
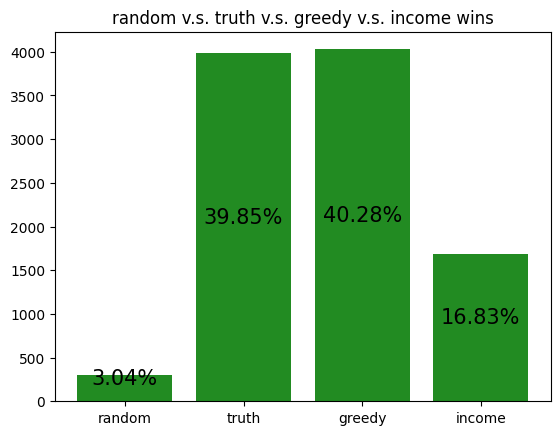
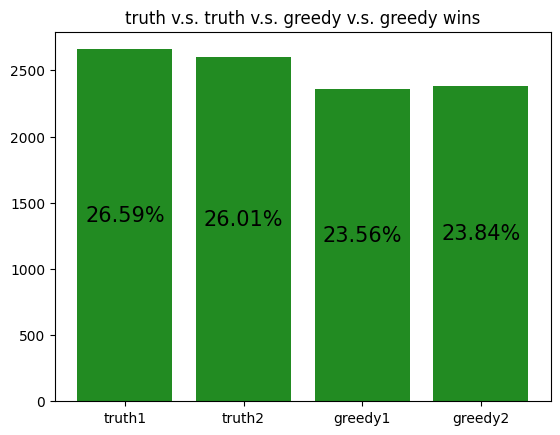
These simulations give us a rough idea of how the archetypes behave amongst themselves, allowing us to potentially gain insight to how our RL agent is learning to play against each of the archetypes.

However, it should be noted that the transitive property does not apply here. For example, although random slightly beats income, and income slightly beats truth, random certainly does not beat truth. Thus, it is not reasonable to assume that training an RL agent to beat one archetype will definitely help it defeat another archetype, even if the first archetype defeats the second.

Implementing Q-Learning

I use the following function to train my Q-Learning agent. It loops through episodes, saving its experiences to the agent's replay buffer until it has enough to update the agent's corresponding Q-Network.

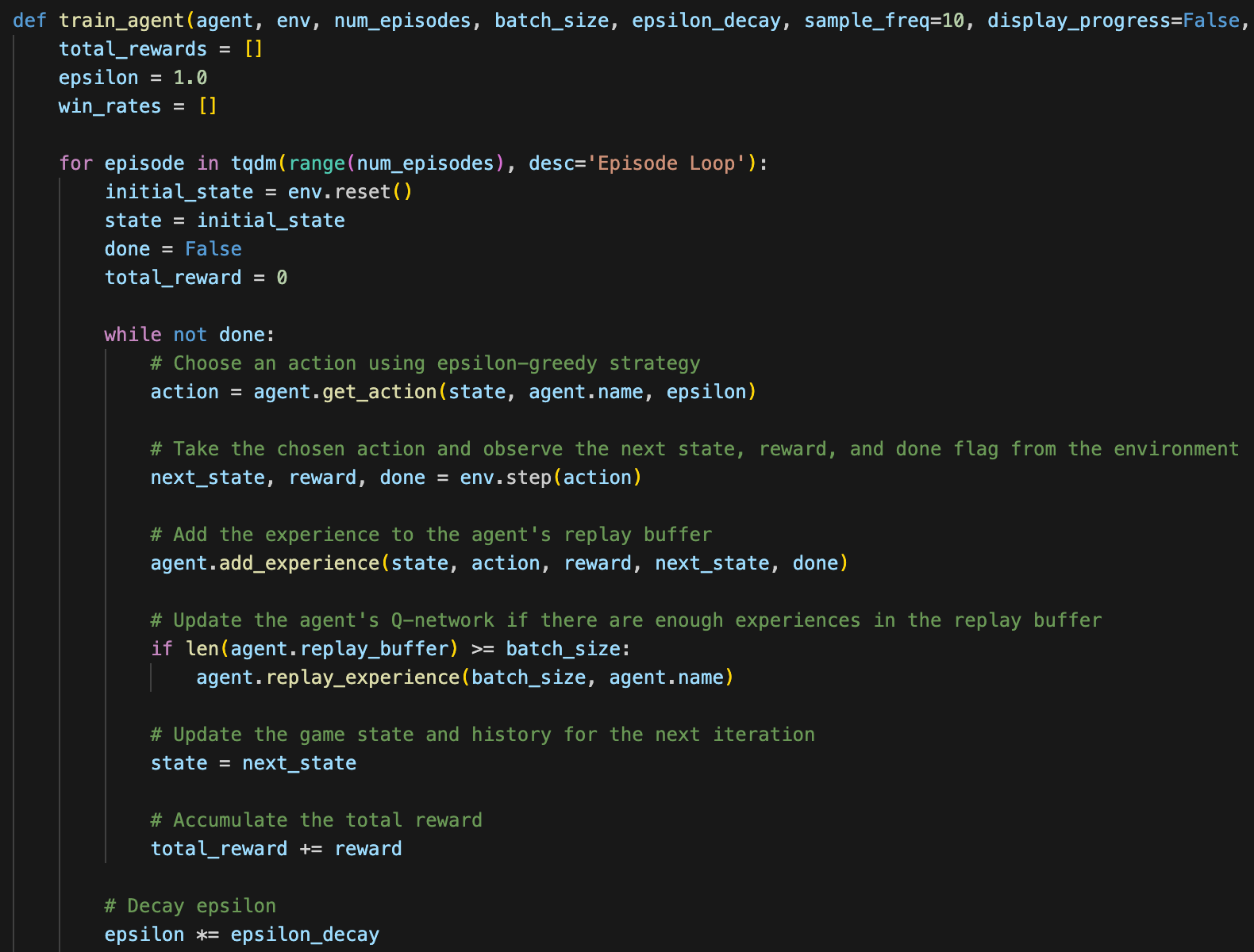
There are two classes that this functions uses: the Environment class and the QLearningAgent class.

The Environment class sets the stage for learning to occur. It has useful functions such as env.reset(), env.step(), etc.

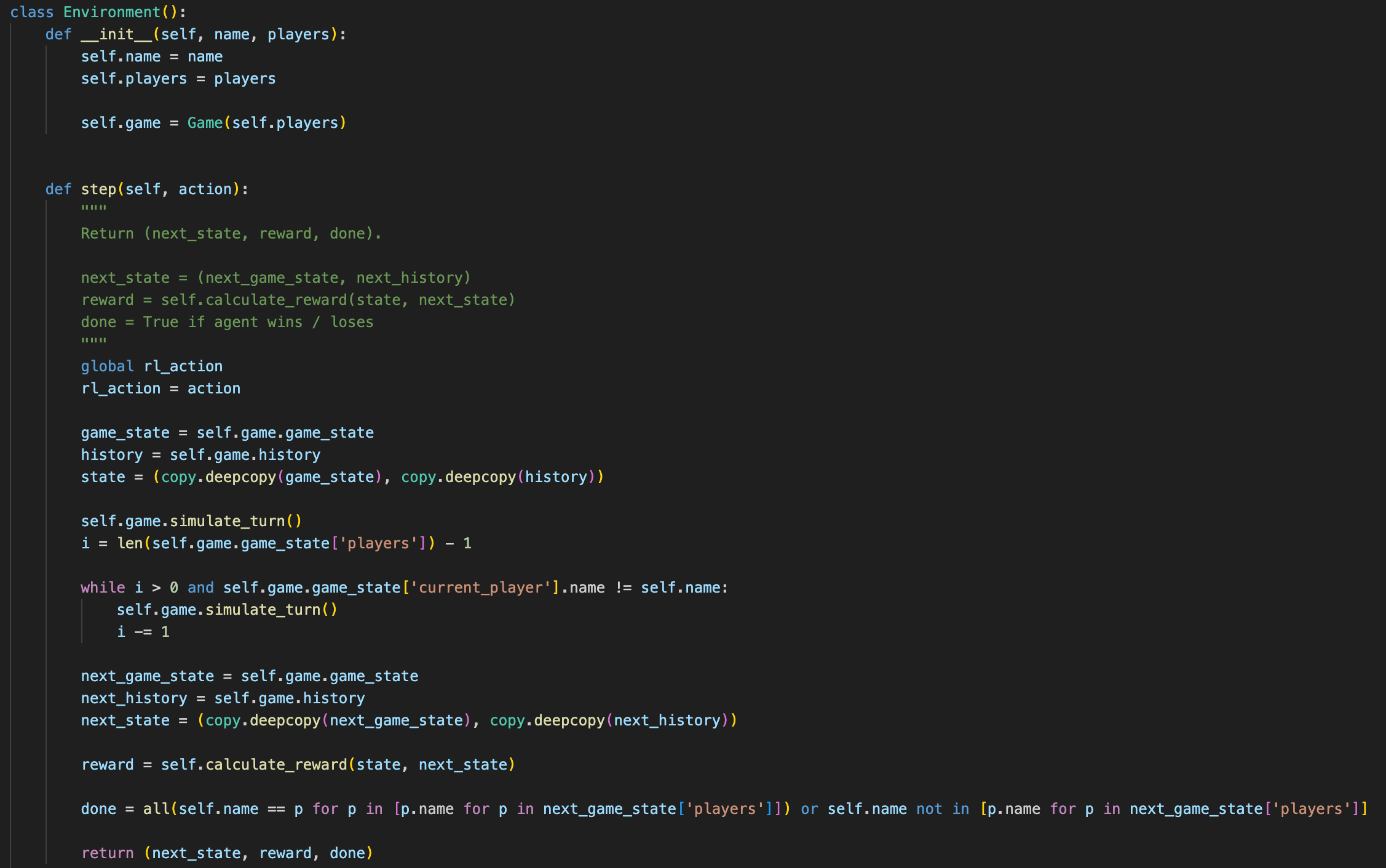
The QLearningAgent class bundles up all of the relevant information for the agent. This is where the Q-Network and replay buffer are stored, and where the Bellman equation is used to update the parameters of the Q-Network.

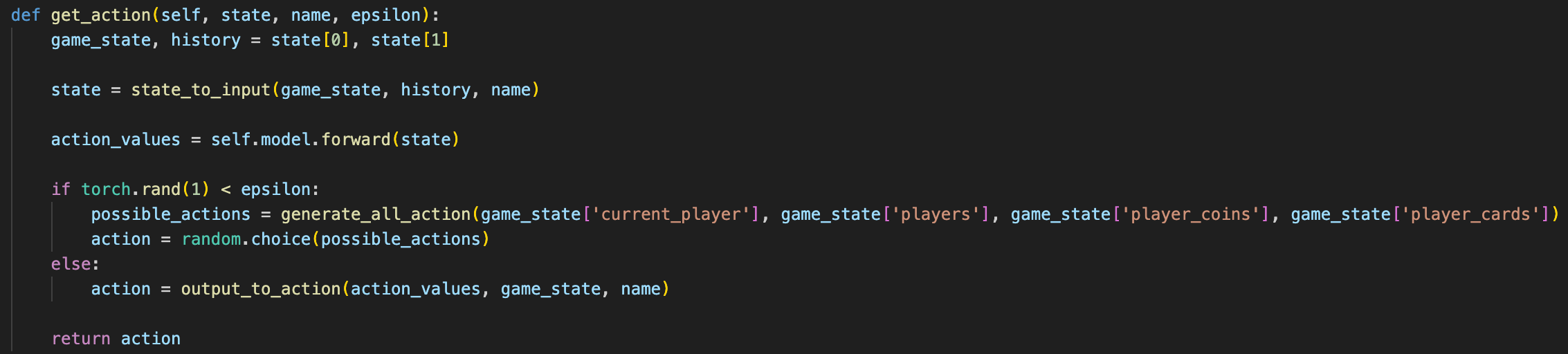
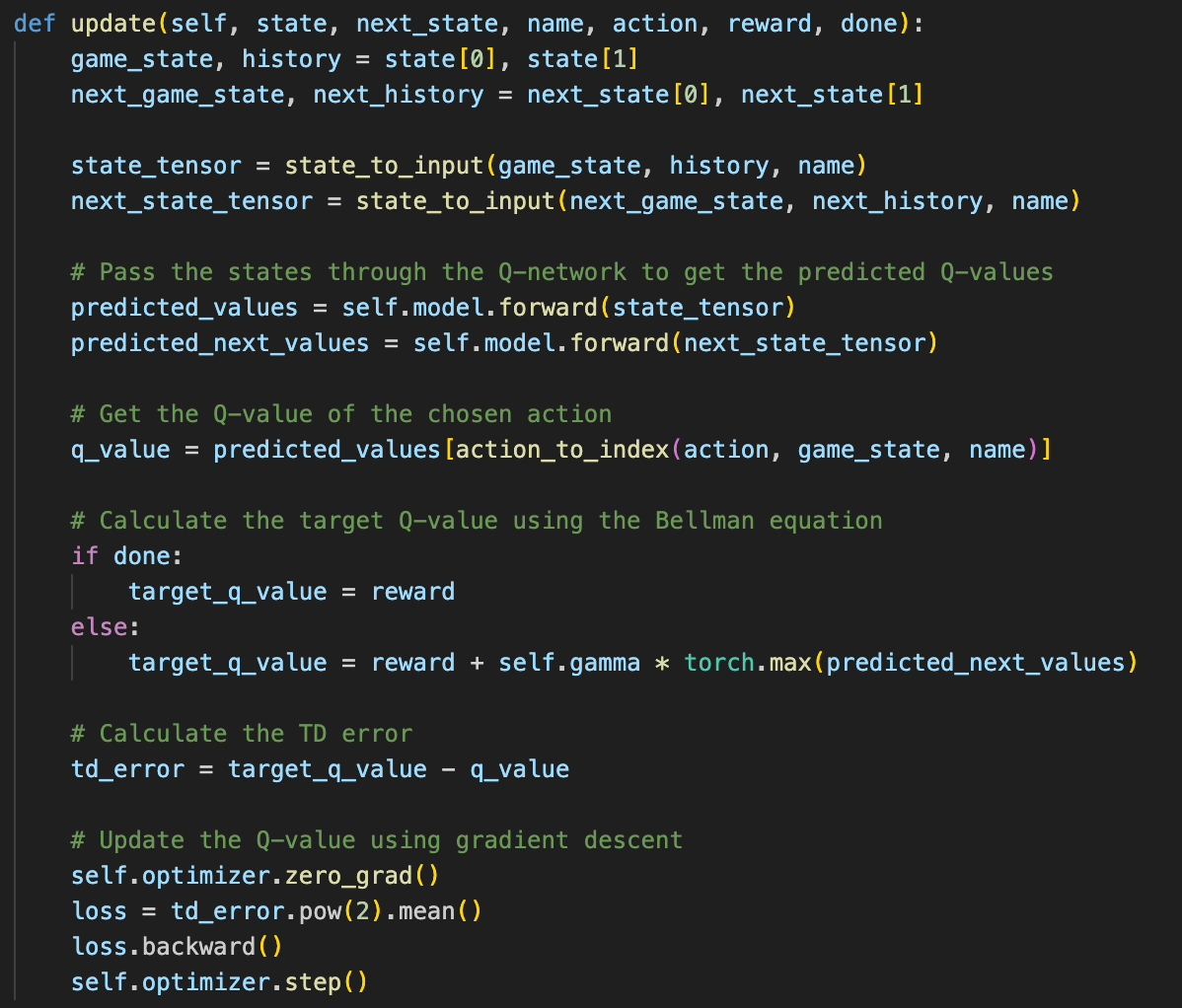
These methods allow the train_agent function to easily interface with the agent and environment, making the code very readable and understandable.

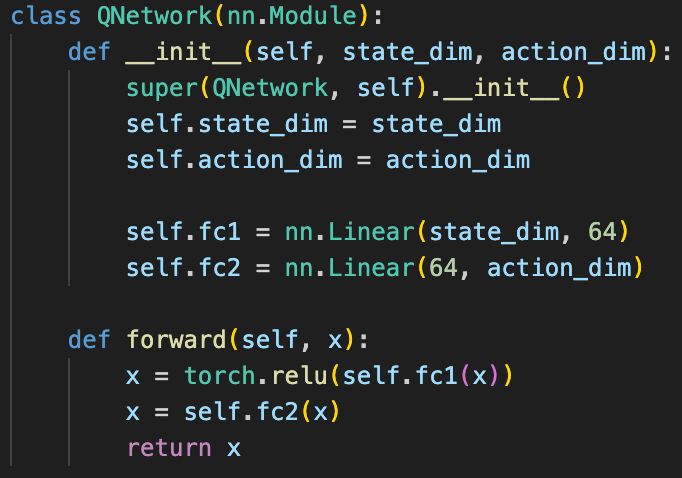
The underlying neural network architecture used for all of my agents was the following:

Note the some elements of this project (the code, the text) were created with assistance from ChatGPT.